Aufbau principle

"Atomic build-up" redirects here. For the spread of nuclear weapons, see Nuclear proliferation.

In atomic physics and quantum chemistry, the Aufbau principle (/ˈaʊfbaʊ/, from German: Aufbauprinzip, lit. 'building-up principle'), also called the Aufbau rule, states that in the ground state of an atom or ion, electrons first fill subshells of the lowest available energy, then fill subshells of higher energy. For example, the 1s subshell is filled before the 2s subshell is occupied. In this way, the electrons of an atom or ion form the most stable electron configuration possible. An example is the configuration 1s² 2s² 2p⁶ 3s² 3p³ for the phosphorus atom, meaning that the 1s subshell has 2 electrons, the 2s subshell has 2 electrons, the 2p subshell has 6 electrons, and so on.

The configuration is often abbreviated by writing only the valence electrons explicitly, while the core electrons are replaced by the symbol for the last previous noble gas in the periodic table, placed in square brackets. For phosphorus, the last previous noble gas is neon, so the configuration is abbreviated to [Ne] 3s² 3p³, where [Ne] signifies the core electrons whose configuration in phosphorus is identical to that of neon.

Electron behavior is elaborated by other principles of atomic physics, such as Hund's rule and the Pauli exclusion principle. Hund's rule asserts that if multiple orbitals of the same energy are available, electrons will occupy different orbitals singly and with the same spin before any are occupied doubly. If double occupation does occur, the Pauli exclusion principle requires that electrons that occupy the same orbital must have different spins (+1⁄2 and −1⁄2).

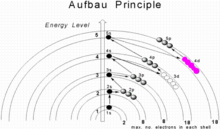
Passing from one element to another of the next higher atomic number, one proton and one electron are added each time to the neutral atom. The maximum number of electrons in any shell is 2n², where n is the principal quantum number. The maximum number of electrons in a subshell is equal to 2(2l + 1), where the azimuthal quantum number l is equal to 0, 1, 2, and 3 for s, p, d, and f subshells, so that the maximum numbers of electrons are 2, 6, 10, and 14 respectively. In the ground state, the electronic configuration can be built up by placing electrons in the lowest available subshell until the total number of electrons added is equal to the atomic number. Thus subshells are filled in the order of increasing energy, using two general rules to help predict electronic configurations:

1. Electrons are assigned to subshells in order of increasing value of n + l.
2. For subshells with the same value of n + l, electrons are assigned first to the subshell with lower n.

A version of the aufbau principle known as the nuclear shell model is used to predict the configuration of protons and neutrons in an atomic nucleus.

Madelung energy ordering rule

The states crossed by same red arrow have same n + l value. The direction of the red arrow indicates the order of state filling.

For multielectron atoms the energy spectra of shells interleave resulting in the n + l rule

In neutral atoms, the approximate order in which subshells are filled is given by the n + l rule, also known as the:

• Madelung rule (after Erwin Madelung)
• Janet rule (after Charles Janet)
• Klechkowsky rule (after Vsevolod Klechkovsky)
• Wiswesser's rule (after William Wiswesser)
• aufbau (building-up) rule or
• diagonal rule

Here n represents the principal quantum number and l the azimuthal quantum number; the values l = 0, 1, 2, 3 correspond to the s, p, d, and f subshells, respectively. Subshells with a lower n + l value are filled before those with higher n + l values. In the many cases of equal n + l values, the subshell with a lower n value is filled first. The subshell ordering by this rule is 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, 8s, 5g, ... For example, thallium (Z = 81) has the ground-state configuration 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹⁰ 5p⁶ 6s² 4f¹⁴ 5d¹⁰ 6p¹ or in condensed form, [Xe] 6s² 4f¹⁴ 5d¹⁰ 6p¹.

Other authors write the subshells outside of the noble gas core in order of increasing n, or if equal, increasing n + l, such as Tl (Z = 81) [Xe]4f¹⁴ 5d¹⁰ 6s² 6p¹. They do so to emphasize that if this atom is ionized, electrons leave approximately in the order 6p, 6s, 5d, 4f, etc. On a related note, writing configurations in this way emphasizes the outermost electrons and their involvement in chemical bonding.

In general, subshells with the same n + l value have similar energies, but the s-orbitals (with l = 0) are exceptional: their energy levels are appreciably far from those of their n + l group and are closer to those of the next n + l group. This is why the periodic table is usually drawn to begin with the s-block elements.

The Madelung energy ordering rule applies only to neutral atoms in their ground state. There are twenty elements (eleven in the d-block and nine in the f-block) for which the Madelung rule predicts an electron configuration that differs from that determined experimentally, although the Madelung-predicted electron configurations are at least close to the ground state even in those cases.

One inorganic chemistry textbook describes the Madelung rule as essentially an approximate empirical rule although with some theoretical justification, based on the Thomas–Fermi model of the atom as a many-electron quantum-mechanical system.

Exceptions in the d-block

The valence d-subshell "borrows" one electron (in the case of palladium two electrons) from the valence s-subshell.

Atom	24Cr	29Cu	41Nb	42Mo	44Ru	45Rh	46Pd	47Ag	78Pt	79Au	103Lr
Core electrons	[Ar]	[Ar]	[Kr]	[Kr]	[Kr]	[Kr]	[Kr]	[Kr]	[Xe] 4f14	[Xe] 4f14	[Rn] 5f14
Madelung rule	3d4 4s2	3d9 4s2	4d3 5s2	4d4 5s2	4d6 5s2	4d7 5s2	4d8 5s2	4d9 5s2	5d8 6s2	5d9 6s2	6d1 7s2
Experimental	3d5 4s1	3d10 4s1	4d4 5s1	4d5 5s1	4d7 5s1	4d8 5s1	4d10	4d10 5s1	5d9 6s1	5d10 6s1	7s2 7p1

For example, in copper ₂₉Cu, according to the Madelung rule, the 4s subshell (n + l = 4 + 0 = 4) is occupied before the 3d subshell (n + l = 3 + 2 = 5). The rule then predicts the electron configuration 1s² 2s² 2p⁶ 3s² 3p⁶ 3d⁹ 4s², abbreviated [Ar] 3d⁹ 4s² where [Ar] denotes the configuration of argon, the preceding noble gas. However, the measured electron configuration of the copper atom is [Ar] 3d¹⁰ 4s¹. By filling the 3d subshell, copper can be in a lower energy state.

A special exception is lawrencium ₁₀₃Lr, where the 6d electron predicted by the Madelung rule is replaced by a 7p electron: the rule predicts [Rn] 5f¹⁴ 6d¹ 7s², but the measured configuration is [Rn] 5f¹⁴ 7s² 7p¹.

Exceptions in the f-block

The valence d-subshell often "borrows" one electron (in the case of thorium two electrons) from the valence f-subshell. For example, in uranium ₉₂U, according to the Madelung rule, the 5f subshell (n + l = 5 + 3 = 8) is occupied before the 6d subshell (n + l = 6 + 2 = 8). The rule then predicts the electron configuration [Rn] 5f⁴ 7s² where [Rn] denotes the configuration of radon, the preceding noble gas. However, the measured electron configuration of the uranium atom is [Rn] 5f³ 6d¹ 7s².

Atom	57La	58Ce	64Gd	89Ac	90Th	91Pa	92U	93Np	96Cm
Core electrons	[Xe]	[Xe]	[Xe]	[Rn]	[Rn]	[Rn]	[Rn]	[Rn]	[Rn]
Madelung rule	4f1 6s2	4f2 6s2	4f8 6s2	5f1 7s2	5f2 7s2	5f3 7s2	5f4 7s2	5f5 7s2	5f8 7s2
Experimental	5d1 6s2	4f1 5d1 6s2	4f7 5d1 6s2	6d1 7s2	6d2 7s2	5f2 6d1 7s2	5f3 6d1 7s2	5f4 6d1 7s2	5f7 6d1 7s2

All these exceptions are not very relevant for chemistry, as the energy differences are quite small and the presence of a nearby atom can change the preferred configuration. The periodic table ignores them and follows idealised configurations. They occur as the result of interelectronic repulsion effects; when atoms are positively ionised, most of the anomalies vanish.

The above exceptions are predicted to be the only ones until element 120, where the 8s shell is completed. Element 121, starting the g-block, should be an exception in which the expected 5g electron is transferred to 8p (similarly to lawrencium). After this, sources do not agree on the predicted configurations, but due to very strong relativistic effects there are not expected to be many more elements that show the expected configuration from Madelung's rule beyond 120. The general idea that after the two 8s elements, there come regions of chemical activity of 5g, followed by 6f, followed by 7d, and then 8p, does however mostly seem to hold true, except that relativity "splits" the 8p shell into a stabilized part (8p_1/2, which acts like an extra covering shell together with 8s and is slowly drowned into the core across the 5g and 6f series) and a destabilized part (8p_3/2, which has nearly the same energy as 9p_1/2), and that the 8s shell gets replaced by the 9s shell as the covering s-shell for the 7d elements.

History

The aufbau principle in the new quantum theory

In the old quantum theory, orbits with low angular momentum (s- and p-subshell) get closer to the nucleus.

The principle takes its name from German, Aufbauprinzip, "building-up principle", rather than being named for a scientist. It was formulated by Niels Bohr in the early 1920s. This was an early application of quantum mechanics to the properties of electrons and explained chemical properties in physical terms. Each added electron is subject to the electric field created by the positive charge of the atomic nucleus and the negative charge of other electrons that are bound to the nucleus. Although in hydrogen there is no energy difference between subshells with the same principal quantum number n, this is not true for the outer electrons of other atoms.

In the old quantum theory prior to quantum mechanics, electrons were supposed to occupy classical elliptical orbits. The orbits with the highest angular momentum are "circular orbits" outside the inner electrons, but orbits with low angular momentum (s- and p-subshell) have high subshell eccentricity, so that they get closer to the nucleus and feel on average a less strongly screened nuclear charge.

Wolfgang Pauli's model of the atom, including the effects of electron spin, provided a more complete explanation of the empirical aufbau rules.

The n + l energy ordering rule

A periodic table in which each row corresponds to one value of n + l (where the values of n and l correspond to the principal and azimuthal quantum numbers respectively) was suggested by Charles Janet in 1928, and in 1930 he made explicit the quantum basis of this pattern, based on knowledge of atomic ground states determined by the analysis of atomic spectra. This table came to be referred to as the left-step table. Janet "adjusted" some of the actual n + l values of the elements, since they did not accord with his energy ordering rule, and he considered that the discrepancies involved must have arisen from measurement errors. As it happens, the actual values were correct and the n + l energy ordering rule turned out to be an approximation rather than a perfect fit, although for all elements that are exceptions the regularised configuration is a low-energy excited state, well within reach of chemical bond energies.

In 1936, the German physicist Erwin Madelung proposed this as an empirical rule for the order of filling atomic subshells, and most English-language sources therefore refer to the Madelung rule. Madelung may have been aware of this pattern as early as 1926. The Russian-American engineer Vladimir Karapetoff was the first to publish the rule in 1930, though Janet also published an illustration of it the same year.

In 1945, American chemist William Wiswesser proposed that the subshells are filled in order of increasing values of the function

$W(n,l)=n+l-{\frac {l}{l+1}}.$

This formula correctly predicts both the first and second parts of the Madelung rule (the second part being that for two subshells with the same value of n + l, the one with the smaller value of n fills first). Wiswesser argued for this formula based on the pattern of both angular and radial nodes, the concept now known as orbital penetration, and the influence of the core electrons on the valence orbitals.

In 1961 the Russian agricultural chemist V.M. Klechkowski proposed a theoretical explanation for the importance of the sum n + l, based on the Thomas–Fermi model of the atom. Many French- and Russian-language sources therefore refer to the Klechkowski rule. '

The full Madelung rule was derived from a similar potential in 1971 by Yury N. Demkov and Valentin N. Ostrovsky. They considered the potential

$U_{1/2}(r)=-{\frac {2v}{rR(r+R)^{2}}}$

where $R$ and $v$ are constant parameters; this approaches a Coulomb potential for small $r$. When $v$ satisfies the condition

$v=v_{N}={\frac {1}{4}}R^{2}N(N+1)$,

where $N=n+l$, the zero-energy solutions to the Schrödinger equation for this potential can be described analytically with Gegenbauer polynomials. As $v$ passes through each of these values, a manifold containing all states with that value of $N$ arises at zero energy and then becomes bound, recovering the Madelung order. The application of perturbation-theory show that states with smaller $n$ have lower energy, and that the s-orbitals (with $l=0$) have their energies approaching the next $n+l$ group.

In recent years it has been noted that the order of filling subshells in neutral atoms does not always correspond to the order of adding or removing electrons for a given atom. For example, in the fourth row of the periodic table, the Madelung rule indicates that the 4s subshell is occupied before the 3d. Therefore, the neutral atom ground state configuration for K is [Ar] 4s¹, Ca is [Ar] 4s², Sc is [Ar] 4s² 3d¹ and so on. However, if a scandium atom is ionized by removing electrons (only), the configurations differ: Sc is [Ar] 4s² 3d¹, Sc⁺ is [Ar] 4s¹ 3d¹, and Sc²⁺ is [Ar] 3d¹. The subshell energies and their order depend on the nuclear charge; 4s is lower than 3d as per the Madelung rule in K with 19 protons, but 3d is lower in Sc²⁺ with 21 protons. In addition to there being ample experimental evidence to support this view, it makes the explanation of the order of ionization of electrons in this and other transition metals more intelligible, given that 4s electrons are invariably preferentially ionized. Generally the Madelung rule should only be used for neutral atoms; however, even for neutral atoms there are exceptions in the d-block and f-block (as shown above).

See also

• Ionization energy

Further reading

• Image: Understanding order of shell filling Archived 2014-11-15 at the Wayback Machine
• Boeyens, J. C. A.: Chemistry from First Principles. Berlin: Springer Science 2008, ISBN 978-1-4020-8546-8
• Ostrovsky, V.N. (2005). "On Recent Discussion Concerning Quantum Justification of the Periodic Table of the Elements". Foundations of Chemistry. 7 (3): 235–39. doi:10.1007/s10698-005-2141-y. S2CID 93589189.
• Kitagawara, Y.; Barut, A.O. (1984). "On the dynamical symmetry of the periodic table. II. Modified Demkov-Ostrovsky atomic model". J. Phys. B. 17 (21): 4251–59. Bibcode:1984JPhB...17.4251K. doi:10.1088/0022-3700/17/21/013.
• Vanquickenborne, L. G. (1994). "Transition Metals and the Aufbau Principle" (PDF). Journal of Chemical Education. 71 (6): 469–471. Bibcode:1994JChEd..71..469V. doi:10.1021/ed071p469.
• Scerri, E.R. (2017). "On the Madelung Rule". Inference. 1 (3). Archived from the original on 2017-04-12. Retrieved 2018-04-15.

External links

• Electron Configurations, the Aufbau Principle, Degenerate Orbitals, and Hund's Rule from Purdue University